By Bruno Ducoudré and Eric Heyer
The industrialized countries are experiencing what seems to be a persistent slowdown in the growth of labour productivity since the second oil shock. This has been the subject of a great deal of analysis in the economic literature[1] that considers the possible disappearance of the growth potential of the developed economies, and consequently their inability to return to a level of activity in line with their pre-crisis trajectories. In other words, could the industrialized countries have entered a phase of “secular stagnation”, making it more difficult to reduce public and private debt? The exhaustion of gains in productivity would also modify any diagnosis made of their conjunctural situation, particularly as regards their labour markets.
Trend productivity gains are inherently unobservable; it is therefore necessary to decompose observed productivity into a trend component and a cyclical component that is linked to the more or less rapid adjustment of employment to changes in economic activity (the productivity cycle). In a recent study published in the Revue de l’OFCE, we seek to highlight the slowdown in trend productivity gains and the productivity cycle in six major developed countries (Germany, Spain, the United States, France, Italy and the United Kingdom) using an econometric method – the Kalman filter – so as to allow the estimation of an equation for labour demand based on explicit theoretical underpinnings and the estimation of trend productivity gains.
After reviewing the various possible explanations for the slowdown described in the economic literature, we present the theoretical modelling of the equation for labour demand and our strategy for an empirical estimation. This equation, derived from a CES-type production function[2], is based on the assumption of maximizing the profit of firms in monopolistic competition and on the assumption of a stable long-term capital-to-output ratio. This makes it possible to break down the trend and cyclical components in a single step, but makes productivity gains depend solely on labour[3].
The existing empirical studies usually rely on a log-linear estimate of the productivity trend and introduce fixed-date trend breaks[4]. We propose an alternative method that consists of writing the employment equation in the form of a state-space model representing the underlying productivity trend. This model has the advantage of allowing a less bumpy depiction of trend productivity gains since it doesn’t rely on ad-hoc break dates.
We then evaluate the new growth path for labour productivity and the productivity cycle for the six countries considered. Our results confirm the slowdown in trend productivity gains (Figure 1).
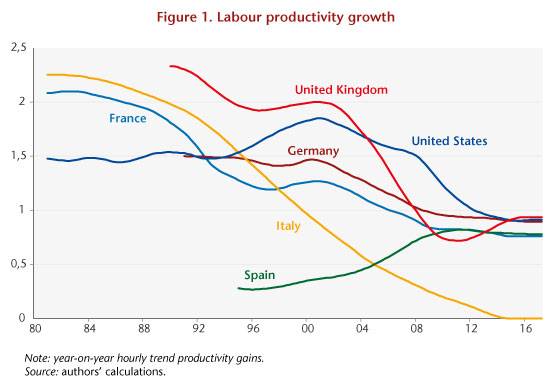
The growth rate for trend productivity for five countries (France, Germany, Italy, the United States and the United Kingdom) shows a slow decline since the 1990s. Trend productivity, estimated at 1.5% in the United States in the 1980s, increased during the 1990s with the wave of new technologies, then gradually decreased to 0.9% at the end of the period. For France, Italy and Germany, the catch-up stopped during the 1990s (during the 2000s for Spain), even though the slowdown in trend productivity gains was interrupted briefly between the mid-1990s and the early 2000s. Leaving aside Italy, whose estimated trend productivity gains were zero at the end of the period, the trend growth rates converged in a range of between 0.8% and 1% in annual trend productivity gains.
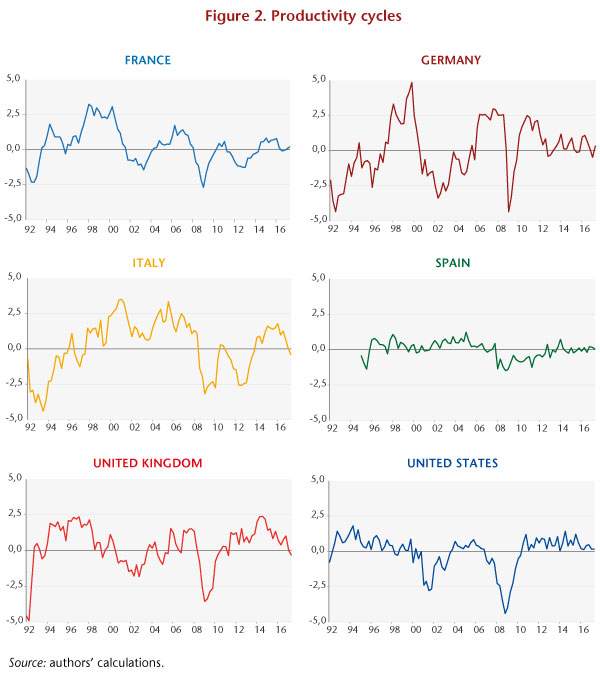
The estimated productivity cycles are shown in Figure 2. They show the greatest fluctuations for France, Italy and Germany and the United Kingdom. A calculation of the average times for the adjustment of employment to demand indicates an adjustment period of 4 to 5 quarters for these countries. The cycle fluctuates much less for the United States and Spain, indicating that the speed of adjustment of employment to economic activity is faster for these two countries, which is confirmed by the average time of adjustment to demand (respectively 2 and 3 quarters). Finally, the estimates indicate globally that the productivity cycle will have closed for each of the countries considered in the second quarter of 2017.
[1] See, for example, A. Bergeaud, G. Cette and R. Lecat, 2016, “Productivity Trends in Advanced Countries between 1890 and 2012”, The Review of Income Wealth, (62: 420-444) and N. Crafts and K. H. O’Rourke, 2013, “Twentieth Century Growth”, CEPR Discussion Papers.
[2] See C. Allard-Prigent, C. Audenis, K. Berger, N. Carnot, S. Duchêne and F. Pesin, 2002, “Présentation du modèle MESANGE”, French Ministère de l’Economie, des finances et de l’industrie, Forecasting Department, MINEFI, Working document.
[3] The equation for labour demand is based on a production function and an assumption of neutral technical progress in Harrod’s sense.
[4] See M. Cochard, G. Cornilleau and E. Heyer, 2010, “Les marchés du travail dans la crise” [Labour Markets in Crisis], Économie et Statistique, (438: 181-204) and B. Ducoudré and M. Plane, 2015, “Les demandes de facteurs de production en France” [The Demand for Production Factors in France], Revue de l’OFCE (142: 21-53).
Leave a Reply